Pengertian Bilangan Pecahan Senilai
Sejarah Pecahan Bilangan pecahan merupakan bilangan yang terdiri dari dua bagian angka, yaitu angka sebagai pembilang (numerator) dan angka sebagai pembagi (denominator). dalam ilmu faraid, pembagi sering disebut sebagai pokok masalah. adapun format penulisan bilangan pecahan ialah: a / b dan b =/ 0 dimana 'a' pembilang 'b' penyebut.
Mesir kuno pecahan pertama kali muncul pada tahun 1600 SM. Pada saat itu masyarakat mesir hanya mengenal satuan. Masyarakat mesir kuno pada saat itu menggunakan penulisan bilangan yang berbeda dari bilangan yang digunakan pada saat ini.
Bangsa babilonia matematika merujuk pada seluruh matematika yang dikembangkan oleh bangsa mesopotania (iraq). Dinamakan matematika babilonia karena kawasan babilonia dikenal sebagai tempat untuk belajar. Pada zaman peradaban helenistik matematika babilonia berpadu dengan matematika yunani dan mesir untuk membangkitkan matematika yunani. matematika babilonia ditulis menggunakan sistem bilangan seksagesimal.
Yunani kuno disebut juga zaman batu, karena pada saat ini manusia masih menggunakan batu untuk menulis. Pada zaman yunani kuno pada dunia ilmu pengetahuan dicirikan oleh know how yang dilandasi pengalaman empiris. kemampuan berhitung menggunakan cara korespondensi satu-satu atau pemetaan. seperti contoh menghitung hewan dikandang dengan kerikil. pada zaman ini bilangan pecahan sangat akrab bagi mereka, hanya saja mereka belum menggunakan pelambangan seperti sekarang ini.
PECAHAN SENILAI
Pecahan merupakan salah satu bilangan yang memiliki bentuk unik. Pecahan ditulia dengan menggunakan 2 bilangan yang disusun vertikal atau atas bawah dengan tanda batas ditengan. Bagian atas disebut “pembilang”, bagian tengah disebut “per” dan bagian bawah disebut “penyebut”.
Pecahan senilai adalah pecahan yang dituliskan dalam bentuk berbeda tetapi mempunyai nilai yang sama.
Perhatikan kedua gambar berikut ini!
Gambar 1 menunjukkan pecahan 2/4 sedangkan gambar 2 menunjukkan pecahan 1/2. Perhatikan juga bahwa bagian besar daerah yang diwarnai pada kedua gambar tersebut sama. Oleh karena itu 2/4 dan 1/2 disebut pecahan senilai.
Pecahan senilai juga disebut pecahan Ekivalen. Untuk dapat lebih mudah memahaminya, mari perhatikan gambar berikut ini.
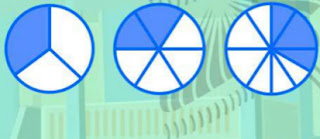
Pada gambar diatas. Gambar “a” merupakan gambar yang ketiga tiganya menunjukkan pecahan senilai. Walaupun antara gambar balok pertama dan kedua bentuk pecahannya berbeda. Begitu juga dengan gambar “b” lingkaran yang dibagi menjadi beberapa bagian.
CARA MENENTUKAN PECAHAN SENILAI DENGAN MEMBAGIKAN ATAU MENGALIKAN PEMBILANG DAN PENYEBUT DENGAN BILANGAN YANG SAMA
Cara untuk menentukan pecahan senilai adalah dengan cara mengalikan atau membagi bilangan pecahan berikut. Perhatikan uraian berikut :
1/1 = 1/2 x 2/2 = 2/4
1/1 = 1/2 x 3/3 = 3/6
1/2 = 1/2 x 4/4 = 4/8
1/2 = 1/2 x 6/6 = 6/12
Dari uraian di atas, dapat dikatakan bahwa pecahan yang senilai dapat diperoleh jika pembilang dan pengebut dari suatu pecahan dikalikan dengan bilangan yang sama. Selanjutnya perhatikan hubungan - hubungan pecahan - pecahan berikut ini :
2/4 = 2/4 : 2/2 = 1/2
3/6 = 3/6 : 3/3 = 1/2
4/8 = 4/8 : 4/4 = 1/2
6/12 = 6/12 : 6/6 = 1/2
Berdasarkan contoh diatas, dapat dikatakan bahwa pecahan yang senilai dapat diperoleh dengan membagi pembilang dan penyebut dari suatu pecahan dengan bilangan yang sama.
Referensi :
Gaffera. (2011). Sejarah Pecahan. 1 juni 2015.
https://online.flipbuilder.com/ameliaa_aini/edts/



Komentar
Posting Komentar