Halo Tematiq! Pernahkah kalian melihat atau mendengar menara Pisa di Italia? Menara Pisa adalah sebuah menara lonceng yang memiliki kemiringan sekitar 50namun tetap berdiri hingga saat ini. Menara Pisa didirikan pada Abad ke-12.
Tahukah kamu, bagaimana menentukan sudut kemiringan dari Menara Pisa ini? Untuk menentukan kemiringan kita bisa menggunakan konsep dari persamaan garis lurus dengan membuat koordinat Kartesiusnya. Aplikasi persamaan garis lurus tidak hanya untuk menentukan kemiringan suatu bangunan namun juga dapat menentukan waktu dan jarak dari kecepatan yang diperoleh, peramalan harga atau jumlah penduduk di tahun tertentu. Menarik, bukan?
So, pada kesempatan kali ini, Aku dan kamu akan membahas tentang garis lurus dan persamaannya, penentuan nilai gradien, serta contoh soa.Yuk, simak!
PENGERTIAN GARIS LURUS & GRADIENT
Garis lurus adalah kumpulan titik-titik yang tak berhingga dan saling berdampingan. Garis lurus dapat dinyatakan ke dalam suatu persamaan eksplisit dan implisit. Persamaan garis lurus secara eksplisit contohnya yaitu y = mx dan y = mx + c sedangkan persamaan garis lurus secara implisit adalah ax + by + c = 0.
Di mana
y = persamaan garis lurus,
m = gradien/ kemiringan,
c = konstanta,
a dan b merupakan suatu variabel.
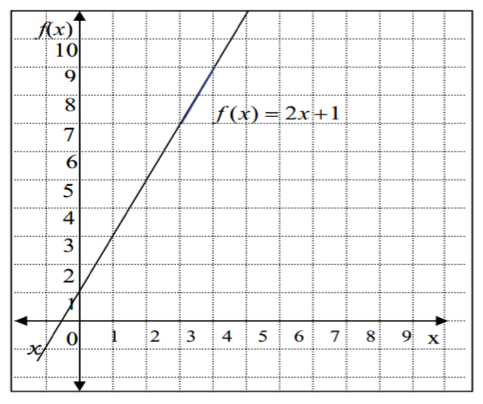
Dari gambar di atas dapat dijelaskan bahwa f(x) = 2x + 1 disebut garis lurus, di mana nilai gradien dari garis tersebut adalah 2 dan konstantanya adalah 1. Garis lurus tersebut berjenis y = mx + c.
Gradien
Gradien adalah nilai kemiringan suatu garis. Gradien dapat bernilai positif atau negatif. Sesuai perjanjian gradien bernilai positif apabila arah garis ke kanan dan ke atas sedangkan gradien bernilai negatif apabila arah garis ke kiri dan ke bawah. Secara umum, nilai suatu gradien garis dapat dinyatakan dalam suatu rumusan matematis yaitu:
Persamaan diatas dapat digunakan apabila garis dihubungkan dengan dua titik X (x2, x1) dan Y (y2, y1). Sedangkan untuk menentukan gradien dari persamaan garis lurus secara implisit (ax + by + c = 0) adalah sebagai berikut:
Apabila suatu soal diketahui nilai gradiennya dan titik koordinatnya A (x1,y1). Maka persamaan garis lurus dapat ditentukan menggunakan persamaan:
Namun apabila di soal terdiri dari dua titik A (x1,y1) dan B (x2,y2). Persamaan garis lurus dapat ditentukan menggunakan persamaan:
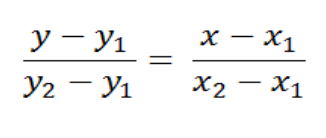
Contoh soal
1. Diketahui garis lurus melalui titik A (-4, 5) dan B (2, 3). Tentukan nilai dari gradien tersebut.
Untuk menjawab soal di atas kita dapat menggunakan rumus persamaan garis di antara dua titik yaitu:
Menentukan Nilai Gradien
Nilai gradien dapat ditentukan dari suatu hubungan dari garis-garis yang ada. Contohnya garis-garis yang sejajar dan garis-garis yang saling tegak lurus. Bunyi hukum gradien suatu garis adalah sebagai berikut “Garis-garis yang sejajar mempunyai gradien yang sama dan hasil kali gradien garis-garis yang saling tegak lurus adalah 1”.
Dari gambar di atas, terlihat ada 4 garis yaitu (garis a, garis b, garis c, dan garis d). Untuk menentukan nilai gradien/kemiringan dari masing-masing tersebut, maka nilai gradiennya dapat diperoleh menggunakan persamaan:
Sehingga gradient garis a adalah
Gradien garis b adalah
Gradien garis c adalah
Gradien garis d adalah
Nilai Gradien dari ke-4 garis tersebut adalah sama yaitu 5/4. Hal ini dikarenakan ke-4 garis tersebut adalah saling sejajar. Sedangkan di bawah ini adalah cara menentukan nilai gradien garis yang saling tegak lurus.
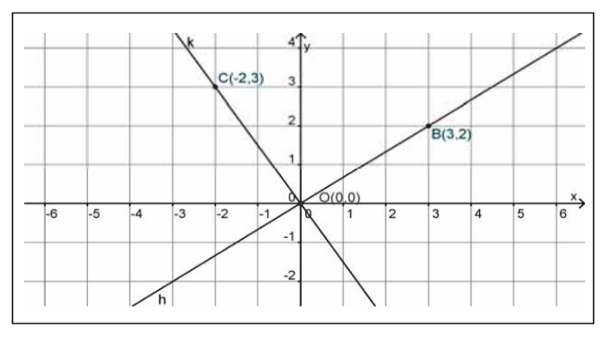
Gradien garis k adalah
Gradien garis h adalah
Perhatikan bahwa perkalian gradien garis h dan garis k diperoleh:
Penerapan konsep dari persamaan garis lurus tidak hanya dapat menentukan nilai kemiringan suatu bangunan namun juga dapat digunakan untuk menentukan permasalahan penting lainnya dalam kehidupan sehari-hari yaitu jarak dan waktu dari suatu kecepatan, peramalan harga suatu barang dalam kurun waktu tertentu, serta peramalan jumlah penduduk dari suatu wilayah. Berikut contoh soal dan pembahasannya.
Sumber:
• Dhoruri,Atmini. 2011. Pembelajaran Persamaan Garis Lurus di SMP.Jakarta: Kemdikbul.
•Insani,Nur.2007.Kalkulus Differensial.Yogyakarta:UniversitasNegeri Yogyakarta



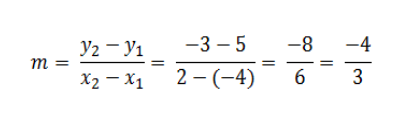




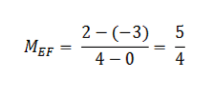


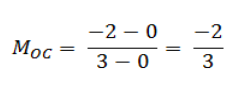


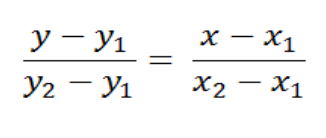

Komentar
Posting Komentar